เนื้อหา

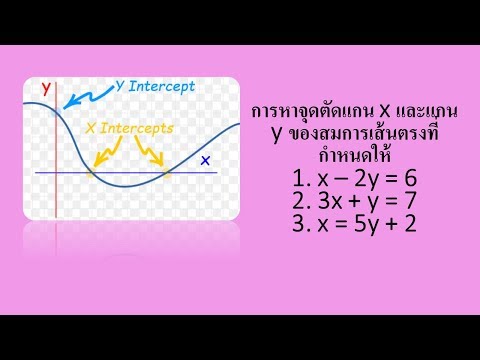
ในคณิตศาสตร์ฟังก์ชันจะอธิบายความสัมพันธ์ระหว่างตัวแปรสองตัวขึ้นไป โดยทั่วไปมีเพียงสองตัวแปร (x และ y) และฟังก์ชันสามารถแสดงบนระนาบคาร์ทีเซียนได้ แกน x คือเส้นแนวนอนโดยที่ค่าของ y เท่ากับศูนย์และแกน y คือเส้นแนวตั้งโดยที่ค่าของ x เท่ากับศูนย์ จุดที่ฟังก์ชันตัดแกน y สามารถพบได้ง่ายโดยรู้ว่า ณ จุดนั้น x เท่ากับศูนย์
ขั้นตอนที่ 1
เขียนสมการทางคณิตศาสตร์ที่อธิบายฟังก์ชัน จากนั้นแยกตัวแปร "y" "ทางด้านซ้ายของสมการ ตัวอย่างเช่นฟังก์ชัน y - (x + 2) ^ 2 = 5 จะถูกเขียนใหม่เป็น y = (x + 2) ^ 2 + 5
ขั้นตอนที่ 2
แทนที่ '' x '' ทั้งหมดทางด้านขวาของสมการด้วยศูนย์ ต่อด้วยตัวอย่างเราจะได้ y = (0 + 2) ^ 2 + 5
ขั้นตอนที่ 3
ดำเนินการและค้นหาค่าของ y; ผลลัพธ์คือจุดที่ฟังก์ชันตัดกับแกน y ในตัวอย่างของเราเราจะพบว่า y = (0 + 2) ^ 2 + 5 = 2 ^ 2 + 5 = 4 +5 = 9