เนื้อหา
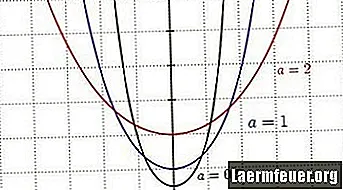
โซ่เป็นรูปทรงที่สายเคเบิลใช้เมื่อได้รับการรองรับโดยปลายและทนต่อน้ำหนักของมันเท่านั้น มีการใช้กันอย่างแพร่หลายในการก่อสร้างโดยเฉพาะสะพานแขวนและมีการใช้ catenary แบบกลับหัวมาตั้งแต่สมัยโบราณในการก่อสร้างซุ้มประตู เส้นโค้ง catenary เป็นฟังก์ชันไฮเพอร์โบลิกโคไซน์ที่มีรูปร่าง "U" คล้ายกับพาราโบลา รูปร่างของ catenary เฉพาะสามารถกำหนดได้จากสเกลแฟกเตอร์
การคำนวณโซ่
ขั้นตอนที่ 1
คำนวณฟังก์ชัน catenary มาตรฐาน y = a cosh (x / a) โดยที่ y คือ y ของระนาบคาร์ทีเซียน x คือ x ของระนาบคาร์ทีเซียน cosh คือฟังก์ชันไฮเพอร์โบลิกโคไซน์และ "a" คือตัวคูณมาตราส่วน
ขั้นตอนที่ 2
สังเกตผลของสเกลแฟคเตอร์ที่มีต่อรูปร่างของโซ่ สามารถคิดเป็นอัตราส่วนของความตึงแนวนอนในสายเคเบิลต่อน้ำหนักของสายเคเบิลต่อความยาวหน่วย จากนั้นสเกลแฟคเตอร์ที่เล็กลงจะทำให้เกิดเส้นโค้งที่ลึกขึ้น
ขั้นตอนที่ 3
คำนวณฟังก์ชัน catenary ด้วยสมการทางเลือก สมการ "y = a cosh (x / a)" สามารถพิสูจน์ได้ว่าเทียบเท่าทางคณิตศาสตร์กับ "y = a / 2 (e ^ (x / a) + e ^ (- x / a))" ซึ่ง "e "เป็นพื้นฐานของลอการิทึมธรรมชาติและมีค่าประมาณ 2.71828
ขั้นตอนที่ 4
คำนวณฟังก์ชันสำหรับ catenary ยืดหยุ่นเช่น "y = yo / (1 + et)" โดยที่ "yo" คือมวลเริ่มต้นต่อความยาวหน่วย "e" คือค่าคงที่ของสปริงและ "t" คือเวลา สมการนี้อธิบายถึงสปริงที่กระเด้งแทนที่จะเป็นสายแขวน
ขั้นตอนที่ 5
คำนวณตัวอย่างจริงของโซ่ ฟังก์ชัน "y = -127.7 cosh (x / 127.7) + 757.7" อธิบายถึง "ประตูโค้งเซนต์หลุยส์" (Arch of St. Louis) ซึ่งมีหน่วยวัดเป็นฟุต