วิธีลดความซับซ้อนของรากที่สอง (อนุมูล)

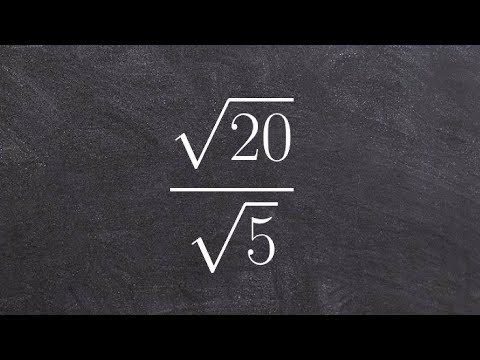
เนื้อหา

• คำสั่ง

งานทั่วไปในพีชคณิตคือการทำให้รากที่สองลดความซับซ้อนหรือที่เรียกว่าอนุมูล บทความนี้จะใช้สัญกรณ์ rqd (x) เพื่อแสดง '' สแควร์รูทของตัวเลข x '' บางครั้งงานการทำให้เข้าใจง่ายค่อนข้างง่าย แต่ในบางงานนั้นจำเป็นต้องใช้สูตรพิเศษควบคู่ไปกับความรู้เกี่ยวกับสี่เหลี่ยมและปัจจัยที่สมบูรณ์แบบ ตัวอย่างเช่นกรณีเช่นนี้จะเป็นรากฐานสำหรับเช่นใน rqd (80) สิ่งนี้มีความสำคัญมากเพราะถ้าหากหัวรุนแรงไม่ง่ายมันจะถือว่าผิดและคุณอาจหรืออาจไม่ได้รับเครื่องหมายบางส่วนสำหรับคำตอบในการทดสอบ บทความนี้คำนึงถึงความคุ้นเคยกับพื้นฐานของการเสริมอำนาจและการแผ่รังสี

คำสั่ง

ความเรียบง่ายของรากที่สองเป็นสิ่งสำคัญในวิชาคณิตศาสตร์ (Jupiterimages / Photos.com / Getty Images)

1. มันง่ายที่จะทำให้หัวรุนแรงง่ายขึ้นซึ่งเป็นรูปสี่เหลี่ยมจัตุรัสที่สมบูรณ์แบบเช่น rqd (81) เราสามารถใช้เครื่องคิดเลขหรือใช้ความรู้ของสี่เหลี่ยมที่สมบูรณ์แบบเพื่อให้ได้ผลลัพธ์ 9 ตั้งแต่9²เท่ากับ 81 เราต้องจำไว้ว่า -9 นั้นเป็นผลลัพธ์สำหรับปัญหาแม้ว่ามันจะถูกทิ้งในบริบทของปัญหาของ เรขาคณิตที่เกี่ยวข้องกับความยาวหรือถ้าเราถูกขอให้ค้นพบสแควร์รูทหลัก

2. ลดความซับซ้อนของอนุมูลอิสระจากจตุรัสที่ไม่สมบูรณ์เช่น rqd (20) ให้ผลงานเพิ่มขึ้นอีกเล็กน้อย เราสามารถใช้เครื่องคิดเลขเพื่อให้ได้ทศนิยมโดยประมาณของคำถาม แต่นั่นไม่ได้ทำให้ความต่างไปจากเดิมอย่างง่าย โดยสรุปสิ่งที่เราถูกขอให้ทำก็คือการแยกอนุมูลอิสระดังนั้นเราจึงได้ผลคูณคูณด้วยสแควร์รูทของตัวเลขตัวแรก

3. ในการทำเช่นนี้ถือเป็นสิ่งสำคัญยิ่งที่จะทราบคุณสมบัติเฉพาะของอนุมูลที่แสดงด้านบน กล่าวอีกนัยหนึ่งสมการบอกเราว่าเราสามารถแยกอนุมูลอิสระของผลิตภัณฑ์ออกจากผลิตภัณฑ์ของอนุมูล ในการใช้สูตรกับตัวอย่างข้างต้นของ rqd (20) เราจะต้องแบ่ง 20 เป็นปัจจัย 4 และ 5 จากนั้นเรามี rqd (4x5) ซึ่งสามารถแยกเป็น rqd (4) x rqd (5) rqd (4) ที่เรารู้คือ 2 ดังนั้นคำตอบที่ง่ายของเราคือ 2 x rqd (5) นี่คือการตอบสนองที่คาดหวังในการตรวจสอบ สังเกตว่าเราไม่สามารถแยกส่วน rqd (5) เนื่องจาก 5 เป็นจำนวนเฉพาะที่หารด้วย 1 และด้วยตัวเองเท่านั้น

   
   

4. บางครั้งนักเรียนถามว่าพวกเขาสามารถแยก 20 เป็นปัจจัยอื่นเช่น 2 และ 10 คำตอบคือเราทำได้ แต่จากนั้นเราจะมี rqd (2x10) ซึ่งจะเป็น rqd (2) x rqd (10) เนื่องจากทั้งสองเป็นสี่เหลี่ยมจัตุรัสที่สมบูรณ์แบบเราจึงไม่มีจำนวนเต็มในคำตอบของเราซึ่งเราต้องมี

5. ลองกลับไปที่ตัวอย่างของ rqd (80) ในบทนำ จำนวน 80 สามารถแยกออกเป็นหลายคู่เช่น 2 และ 40, 4 และ 20, 8 และ 10 เป็นต้น สิ่งที่เราต้องมองหาคือปัจจัยที่ใหญ่ที่สุดของสี่เหลี่ยมจัตุรัสที่สมบูรณ์แบบของ 80 และใช้มัน หมายเลข 4 เป็นตัวประกอบกำลังสองที่สมบูรณ์แบบของ 80 แต่มีตัวที่ใหญ่กว่า: 16 ซึ่งหมายความว่าเราควรใช้ 16 และ 5 ในการหยุดแฟคตอริ่งของเรา ตอนนี้เรามี rqd (16 x 5) = rqd (16) x rqd (5) = 4 x rqd (5) ซึ่งเป็นคำตอบของเรา

6. ในตัวอย่างข้างต้นถ้าเราใช้ 40 และ 20 กับหนึ่งในคู่ปัจจัยของเราเราจะมีงานพิเศษมากมายให้ทำด้วย rqd (4) x rqd (20) ซึ่งเท่ากับ 2 x rqd (20) แต่เราต้องหา rqd (20) เหมือนที่เคยทำมาก่อน ด้วยการใช้ตัวคูณกำลังสองที่สมบูรณ์แบบที่สุดเราสามารถตอบสนองได้เล็กน้อย

7. ตัวอย่างอื่น: rqd (200) มีหลายปัจจัยหลายแห่งเป็นสี่เหลี่ยมที่สมบูรณ์แบบ เราต้องการตัวคูณกำลังสองที่สมบูรณ์แบบที่สุดซึ่งก็คือ 100 นี่ให้ rqd (100) x rqd (2) เหมือนกับ 10 x rqd (2)

   
   

8. โปรดทราบว่าเราไม่สามารถลดค่าสแควร์รูทของจำนวนที่เป็นไพร์มหรือเป็นผลคูณของจำนวนเฉพาะสองจำนวน ตัวอย่างเช่นเราไม่สามารถลดความซับซ้อนของ rqd (13) มันเป็นจำนวนเฉพาะที่ไม่มีตัวประกอบกำลังสองที่สมบูรณ์แบบ เราต้องทิ้งคำตอบไว้เช่นนี้

   อีกตัวอย่างหนึ่งคือ rqd (6) หกไม่ได้เป็นนายก เราสามารถแยกใน rqd (2) x rqd (3) แต่ไม่มีของใดที่เป็นรูปสี่เหลี่ยมจัตุรัสที่สมบูรณ์แบบดังนั้นเราจึงไม่สามารถทำให้ง่ายขึ้นได้ เราจะทิ้งคำตอบไว้เป็น rqd (6) มันไม่ได้มีปัจจัยสแควร์ที่สมบูรณ์แบบใด ๆ ตัวอย่างสุดท้ายคือ rqd (77) จำนวน 77 นั้นไม่ได้สำคัญเพราะมันมีปัจจัยที่เกิน 1 และตัวของมันเอง แต่ปัจจัยอื่น ๆ เหล่านี้มีความสำคัญ เนื่องจากมันไม่มีตัวประกอบกำลังสองที่สมบูรณ์แบบเราจึงต้องปล่อยให้คำตอบนั้นเป็นสิ่งที่ถูกต้อง