
เนื้อหา
- กำหนดเวลาในอากาศ
- ขั้นตอนที่ 1
- ขั้นตอนที่ 2
- ขั้นตอนที่ 3
- ขั้นตอนที่ 4
- กำหนดความสูงสูงสุด
- ขั้นตอนที่ 1
- ขั้นตอนที่ 2
- ขั้นตอนที่ 3
- กำหนดระยะทางแนวนอนที่เดินทาง
- ขั้นตอนที่ 1
- ขั้นตอนที่ 2
- ขั้นตอนที่ 3
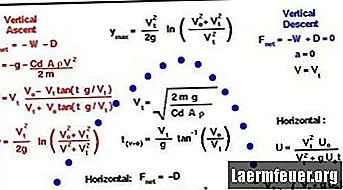
นี่คือวิธีการคำนวณวิถีของกระสุนและโดยเฉพาะเวลาในอากาศช่วงและจุดสูงสุดของวิถี ในตัวอย่างนี้มีการตั้งสมมติฐานเพื่อลดความซับซ้อนของการคำนวณ: แรงต้านอากาศเล็กน้อยไม่มีลมและระยะยิงไม่เพียงพอที่การหมุนของโลกจะมีผล
กำหนดเวลาในอากาศ
ขั้นตอนที่ 1
ขั้นแรกต้องกำหนดรูปร่างของคันธนู หากเริ่มแรกมุมลงแสดงว่าจุดสูงสุดเป็นตำแหน่งยิงแล้ว แม้แต่มุมที่สูงขึ้นก็สามารถกำหนดให้เป้าหมายเป็นจุดสูงสุดได้ไม่ว่ามุมนี้จะตื้นหรือมีความสูงเพียงพอ (h) สิ่งนี้สามารถกำหนดได้ในขั้นตอนที่ 4 เมื่อกำหนดเวลาออกอากาศ
ขั้นตอนที่ 2
ถ้ามุม "?" อัตราการยิงคือระหว่างวิถีเริ่มต้นของโพรเจกไทล์และแนวนอนดังนั้นความเร็วแนวตั้งเริ่มต้นคือ V (i) = V.sen?
ขั้นตอนที่ 3
พบเวลาออกอากาศโดยใช้สมการของตำแหน่ง h = V.sen? .T - (0.5) g.t ^ 2 โดยที่ g = 9.8 เมตร / วินาที ^ 2 รู้จักตัวแปรทั้งหมดยกเว้นเวลาในอากาศ t ดังนั้นจึงสามารถแก้ไขได้โดยใช้ฟังก์ชันกำลังสอง: ax ^ 2 + bx + c = 0 ดังนั้น x = [-b ±√ (b ^ 2-4ac )] / 2a
ขั้นตอนที่ 4
หากอนุญาตให้ใช้วิธีแก้ปัญหามากกว่าหนึ่งวิธีตั้งแต่ h> 0 ผลลัพธ์แรกจะสอดคล้องกับเมื่อ height = h บนเส้นทางขึ้นและครั้งที่สองเมื่อ height = h บนเส้นทางการสืบเชื้อสาย ถ้า h <0 แสดงว่าวิธีแก้ปัญหาจริงเพียงวิธีเดียวสำหรับ t ได้รับอนุญาตและอีกทางหนึ่งเป็นลบ
กำหนดความสูงสูงสุด
ขั้นตอนที่ 1
ถ้า? <0 เป็นที่ทราบกันดีอยู่แล้วว่าความสูงสูงสุดคือความสูงเริ่มต้น h = 0
ขั้นตอนที่ 2
หากมีมากกว่าหนึ่งครั้ง t ซึ่งสัญลักษณ์แสดงหัวข้อย่อยขยาย h ดังนั้น t ที่เล็กที่สุดจะตรงกับเส้นทางการบินโดยที่ h คือจุดสูงสุด t ที่ใหญ่ที่สุดสอดคล้องกับสัญลักษณ์แสดงหัวข้อย่อยที่ถึงความสูงที่สูงขึ้นก่อนที่จะกลับไปที่ h เพื่อแก้ปัญหาความสูงนี้จะใช้สูตร V (t) = V (0) - 9.8t เพื่อหาค่าของ t เมื่อความเร็วในแนวตั้งคือ ศูนย์. กล่าวอีกนัยหนึ่ง t, V.sen? = 9.8t.?
ขั้นตอนที่ 3
การแก้ t และการเชื่อมต่อสูตรความสูงเรามีความสูงสูงสุด: hm = V.sen? - 4.9 ครั้ง ^ 2 วิธีการเดียวกันนี้ใช้สำหรับการแก้ปัญหาความสูงสูงสุดหากอนุญาตให้ใช้โซลูชันเดียวสำหรับ t
กำหนดระยะทางแนวนอนที่เดินทาง
ขั้นตอนที่ 1
หากต้องการกำหนดระยะทางแนวนอนตามเวลาที่สัญลักษณ์แสดงหัวข้อย่อยถึงความสูง h อันดับแรกให้คำนวณความเร็วแนวนอนเริ่มต้นของสัญลักษณ์แสดงหัวข้อย่อย: v (i) = V.cos (?)
ขั้นตอนที่ 2
แทนเวลา t เมื่อสัญลักษณ์แสดงหัวข้อย่อยถึงความสูงสุดท้าย A ในตำแหน่งของสูตรโดยใช้ความเร็วแนวนอน: A = V.cosΘ.t. สมมติว่าไม่มีแรงต้านอากาศและไม่มีระยะเร่งทางด้านขวา
ขั้นตอนที่ 3
ถ้ามีมากกว่าหนึ่งครั้ง t เมื่อความสูงอยู่ใน h ตำแหน่งทั้งสองของ "A" จะถูกต้องโดยจุดสูงสุดที่ถึงคือ hm สำหรับค่าที่เล็กกว่าของ "A" ทั้งสอง ขณะนี้ทราบตำแหน่งปลายแนวนอนและแนวตั้งและจุดสูงสุดที่ถึงแล้วจึงกำหนดวิถีกระสุน