
เนื้อหา
ตรีโกณมิติเป็นการศึกษาทางคณิตศาสตร์ของรูปสามเหลี่ยม ในนั้นการวัดของมุมที่ไม่รู้จักในรูปสามเหลี่ยมเรียกว่าสามเหลี่ยม theta (θ) การวัดมุมθสามารถกำหนดได้ด้วยการใช้อัตลักษณ์ตรีโกณมิติ
คำสั่ง
-
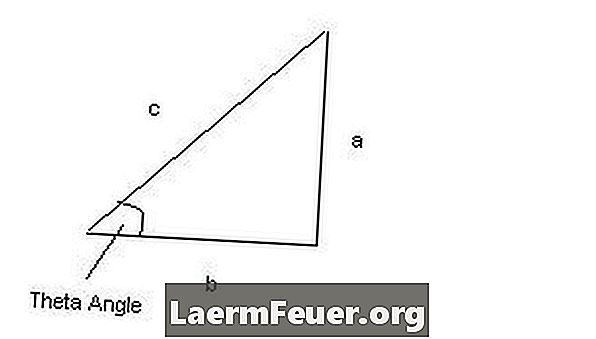
ระบุมุมθซึ่งเป็นมุมที่ไม่รู้จักของรูปสามเหลี่ยม
-
ระบุด้าน "a", "b" และ "c" ของรูปสามเหลี่ยม ด้าน "a" คือด้านตรงข้ามของมุมทีต้า ด้าน "b" คือด้านที่อยู่ติดกับมุมθ ด้าน "c" คือด้านตรงข้ามมุมฉากหรือด้านที่ใหญ่กว่าของรูปสามเหลี่ยม
-
เลือกอัตลักษณ์ตรีโกณมิติเพื่อหามุม according ตามขนาดของด้านที่รู้จัก ตรีโกณมิติคือ: 1. sin (θ) = a / c 2. cos (θ) = b / c 3. tan (θ) = a / b
-
วางมิติของด้านข้างสำหรับข้อมูลเฉพาะตัวเกี่ยวกับวิชาตรีโกณมิติที่เลือกเพื่อกำหนดสัดส่วน ตัวอย่างเช่นถ้าด้าน a = 6 และด้าน c = 10, sin (θ) = 6/10 หรือ 0.6
-
การใช้เครื่องคิดเลขแบบกราฟิกหรือวิทยาศาสตร์ให้ใช้อัตราส่วนของตัวตนเพื่อกำหนดค่าของมุม angle ในเครื่องคิดเลขให้เลือกปุ่ม sin ^ -1, cos ^ -1 หรือ tan ^ -1 ตามข้อมูลตรีโกณมิติที่ใช้และป้อนอัตราส่วนที่พบในขั้นตอนก่อนหน้า การตอบสนองต่อฟังก์ชั่นนี้คือการวัดมุมθ ตัวอย่างเช่นถ้า sin (θ) = 0.6 ดังนั้น sin ^ -1 (0.6) = 36.9 และมุมθวัด 36.9 องศา
การเตือน
- มุมสามารถวัดได้ในเรเดียนหรือองศา เลือกหน่วยวัดที่เหมาะสมบนเครื่องคิดเลขก่อนเริ่ม
สิ่งที่คุณต้องการ
- เครื่องคิดเลขแบบกราฟิกหรือวิทยาศาสตร์